控制系统稳定性

控制系统的稳定性被定义为当有界输入作用于任何系统时，它提供有界输出的能力。更具体地说，我们可以说，稳定性允许系统达到稳态，并且即使在系统的参数发生变化后，对于特定的输入仍然保持在该状态。

稳定性被认为是控制系统的一个重要特性。也称为系统达到稳态的能力。

由于它是控制系统的一个重要特性，因此控制系统的性能对稳定性具有高度的依赖性。

介绍

我们已经学过了控制系统，即控制系统的各个单元联合操作，从而为系统提供特定的输出。

为了得到指定的输出，必须对系统的各个参数进行控制。与此同时，系统必须足够稳定，使输出不受系统参数的不期望变化或干扰的影响。

因此，我们可以说设计一个稳定系统是为了使系统的响应不随系统参数的变化而发生不可容忍的变化。

这里要注意的是，稳定性或不稳定性是控制系统的特性，因此取决于闭环系统的极点。

因此，我们可以说稳定性是系统的一个因素，它与系统的输入无关。然而，系统的稳态输出依赖于应用输入的极点。

控制系统稳定性

我们已经讨论过，一个稳定的系统对有界的输入产生有界的输出(BIBO)。

现在问题来了什么是有界信号?

一个信号的有界值代表一个有限值。更具体地说，我们可以说，有界信号具有一个有限的最大值和最小值。因此，如果任何信号的最大值和最小值都是有限的，那么这就意味着在最大值和最小值之间的所有其他值也是有限的。

假设我们有一个如下所示的信号:

正如我们所看到的，这里信号的最大值和最小值都是有限的。因此，这样的信号被称为有界的，如果这样的输出是由一个系统提供的，那么它就是一个稳定的系统。

因此，反过来，我们可以说，当应用的输入在本质上是有界的时，一个不稳定的系统提供了一个无界的输出。

那么什么是无界信号呢?

因此，一般来说，图上显示连续上升从而显示无限值的信号，如斜坡信号，称为无界信号。下图为无界信号:

有时我们会遇到渐近稳定系统它定义为当输入不存在时，即使系统的参数发生变化，其输出也为0的系统。

这里要指出的是的两极传递函数，是决定控制系统稳定性的一个因素。

现在的问题是，极点如何给出关于系统稳定性的信息吗?

• 当系统的传递函数的极点位于s平面的左侧时，就说它是一个稳定的系统。然而，当极点向0或原点移动时，在这种情况下，系统的稳定性下降。
  
• 在虚轴上存在的极点有两种情况:

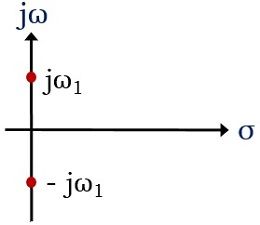
1. 如果对一个系统来说，极点在虚轴上并且本质上是不重复的，那么它就是a稍微稳定的系统。
   
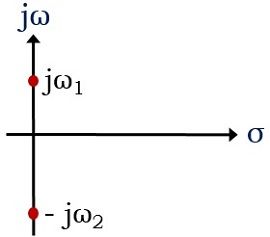
2. 但是，如果在s平面的虚轴上存在重复的极点。然后它被称为an不稳定的系统。
   

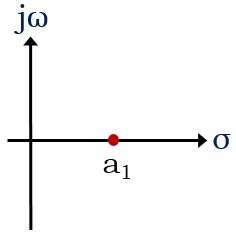
• 如果一个系统在s平面的右域中有极点，那么这样的系统称为不稳定系统。即使在右半部分只存在一个磁极，也会使系统不稳定。
  
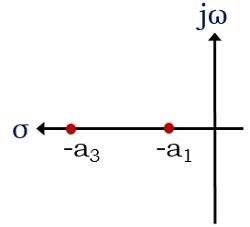
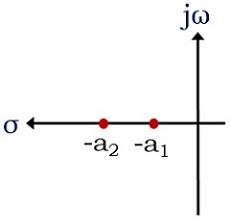
• 出现在原点附近的两极就叫做占主导地位的波兰人。因此，如果一个稳定的系统有-a极₁和一₂然后,一₁被认为是那个特定系统的主导极点。
  

• 一个系统被认为是一个不稳定的系统，如果它的输出不接近0，因此即使在没有输入的情况下也表示某个值。

因此，我们可以说s平面上极点的位置与系统的稳定性相对应。

稳定系统的类型

• 绝对稳定的系统:绝对稳定系统是即使系统的参数变化也能提供有界输出的系统。也就是说，这种系统的输出在达到稳态后不随扰动或系统参数值的变化而变化。

下图为绝对稳定系统的阶跃响应:

在绝对稳定的情况下，极点的性质必须是真实的和负的。

下图是一个不稳定的系统:

• 有条件稳定的系统:一个条件稳定的系统对由系统参数定义的系统的唯一特定条件给出有界输出。

因此，我们可以说，系统只有在特定条件下才具有稳定性。

如果违反了这个条件系统就会产生无界输出。

• 临界稳定系统边缘稳定系统是指当有界输入时，产生频率和振幅不变的信号的系统。

这些振荡被称为持续振荡。图中表示了边际稳定系统的阶跃响应:

闭环极点的性质必须是非重复的，并且位于虚轴上。

在此基础上，研究了控制系统的稳定性。